Introduction

The Three-Body Problem is nothing more than the Two-Body Problem with one more body added to the system.

Consider a system with three finite masses and some origin in the inertial frame of reference:

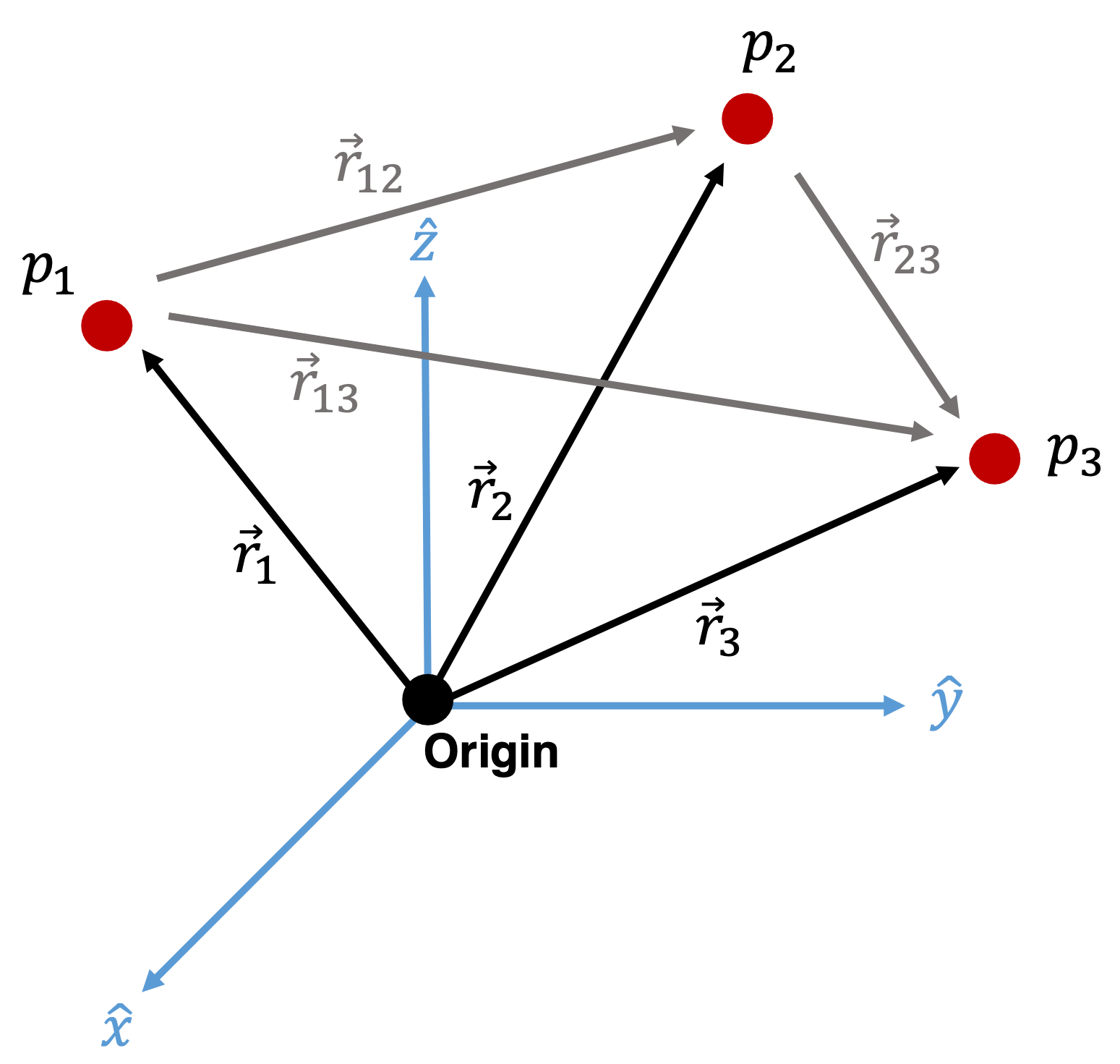
Figure 1.1 Three-Body Problem Definition

Such that the body masses are non-zero: $P_1$ has mass $m_1$, $P_2$ has mass $m_2$, and $P_3$ has mass $m_3$. Define the general relative vector notation as.

(1)$${\mathbf{r}}_{ij}={\mathbf{r}}_j-{\mathbf{r}}_i$$

For example

$${\mathbf{r}}_{12}={\mathbf{r}}_2-{\mathbf{r}}_1$$

and

$${\mathbf{r}}_{12}=-{\mathbf{r}}_{21}$$

We are interested in how vectors ${\mathbf{r}}_1$, ${\mathbf{r}}_2$, and ${\mathbf{r}}_3$ change as a function of time. Assuming they only interact gravitationally and each particle has a uniform spherical gravitational field.

From Newton’s Law of Gravitation, the mutual gravitational interaction on one finite point mass due to the other masses is:

(2)$$m_i{\ddot{\mathbf{r}}}_i={\mathbf{F}}_{\mathbf{ij}}+{\mathbf{F}}_{\mathbf{ik}}$$

For the Three-Body System the three force interactions are:

(3)$$m_1{\ddot{\mathbf{r}}}_1=-G\frac{(m_1{m}_2)}{r_{21}^3}{\mathbf{r}}_{\mathbf{21}}-G\frac{(m_1{m}_3)}{r_{31}^3}{\mathbf{r}}_{\mathbf{31}}$$

(4)$$m_2{\ddot{\mathbf{r}}}_2=-G\frac{(m_2{m}_1)}{r_{12}^3}{\mathbf{r}}_{\mathbf{12}}-G\frac{(m_2{m}_3)}{r_{32}^3}{\mathbf{r}}_{\mathbf{32}}$$

(5)$$m_3{\ddot{\mathbf{r}}}_3=-G\frac{(m_3{m}_1)}{r_{13}^3}{\mathbf{r}}_{\mathbf{13}}-G\frac{(m_3{m}_2)}{r_{23}^3}{\mathbf{r}}_{\mathbf{23}}$$

These are equations of motion for the Three-Body Problem.

Note

The Solar System Dynamics group at NASA JPL keeps track of parameters commonly used in Astrodynamics. Among the parameters listed on the Astrodynamics Parameters page is the Newtonian Constant of Gravitation ($G$).

$$G=6.67430(\pm 0.00015)\times {10}^{-11}k{g}^{-1}{m}^3{s}^{-2}$$

Another reference of interest for the Three-Body Problem is the Physical Parameters of Planets page. There you will find a useful reference for the mass of a planetary body used in astrodynamic computations.

Each particle has a State Vector made up of its position and velocity:

(6)$$\begin{array}{r}\mathbf{x}=\left[\begin{array}{c}x\\ y\\ z\\ \dot{x}\\ \dot{y}\\ \dot{z}\end{array}\right]\end{array}$$

To solve the for the Three-Body Problem we require 18 equations of motion due to 3 particle state vectors. Unfortunately, there are only 10 Classical Integrals available. The Three-Body Problem is a non-trivial problem, and generally, a non-integrable problem in dynamics.

The next sections will introduce a special case Three-Body Problem that is better formulated for numerical analysis. First let us introduce the Jacobian Coordinate Frame.

Jacobian Coordinate Frame

To help derive the equations of motion for the restricted Three-Body Problem, consider the Jacobi Coordinate formulation. Which is defined such that $P_3$ is with respect to the barycenter of the other two particles by attaching a non-inertial coordinate system to the barycenter of $P_1$ and $P_2$ as shown in the figure below:

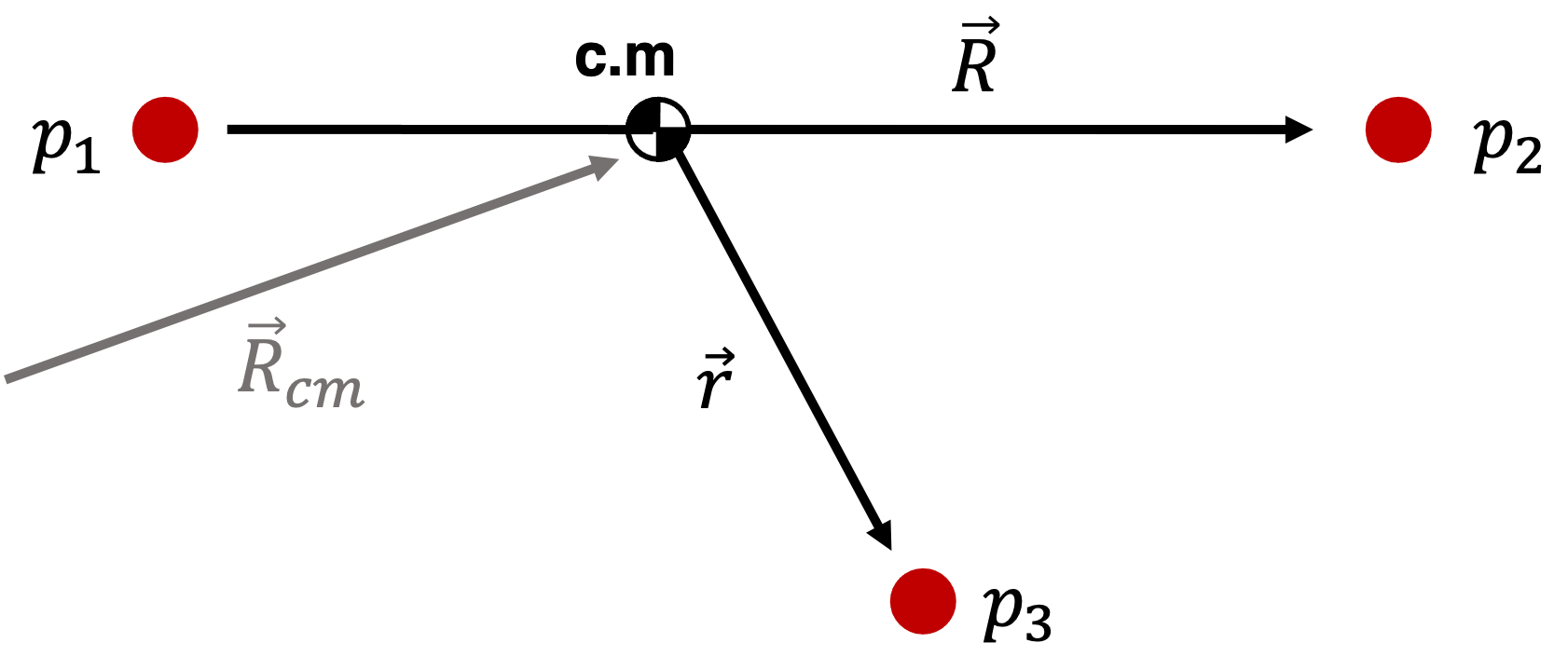
Figure 1.2 Jacobi Coordinate Frame

Where the center of mass of $P_1$ and $P_2$ is defined as vector ${\mathbf{R}}_{cm}$

(7)$${\mathbf{R}}_{cm}=\frac{m_1{\mathbf{r}}_1+m_2{\mathbf{r}}_2}{m_1+m_2}$$

$\mathbf{R}$ is the positional vector from $P_1$ to $P_2$

(8)$$\mathbf{R}={\mathbf{r}}_{12}={\mathbf{r}}_2-{\mathbf{r}}_1$$

and the positional vector of $P_3$ relative to the barycenter is defined as

(9)$$\mathbf{r}={\mathbf{r}}_3-{\mathbf{R}}_{cm}$$

Note

The Earth-Moon system is a classic example of using the Jacobian Coordinate Frame. Where $P_1$ and $P_2$ represent the Earth and Moon, and $P_3$ can be considered a spacecraft relative to the Earth-Moon system.

By taking the derivative of Equation (8), Equation (9) and utilizing the Equations (3) - (5) we end up with the following two equations of motion:

(10)$$\ddot{\mathbf{R}}=-G(m_1+m_2)\frac{\mathbf{R}}{R^3}+G{m}_3[\frac{\mathbf{r}-\frac{m_1}{m_1+m_2}\mathbf{R}}{|\mathbf{r}-\frac{m_1}{m_1+m_2}\mathbf{R}{|}^3}-\frac{\mathbf{r}+\frac{m_2}{m_1+m_2}\mathbf{R}}{|\mathbf{r}+\frac{m_2}{m_1+m_2}\mathbf{R}{|}^3}]$$

(11)$$\ddot{\mathbf{r}}=-G\frac{(m_1+m_2+m_3)}{m_1+m_2}[\frac{m_1(\mathbf{r}+\frac{m_2}{m_1+m_2}\mathbf{R})}{|\mathbf{r}+\frac{m_2}{m_1+m_2}\mathbf{R}{|}^3}+\frac{m_2(\mathbf{r}-\frac{m_1}{m_1+m_2}\mathbf{R})}{|\mathbf{r}-\frac{m_1}{m_1+m_2}\mathbf{R}{|}^3}]$$

This is a very complicated solution to the equations of motion for the Jacobian Coordinate frame. Generally, it is useful to assume the third particle has zero or negligible mass.

$$m_3\to 0$$

Which is certainly a valid assumption when analyzing satellite dynamics in the Earth-Moon system.