Circular Restricted Three-Body Problem

By letting \(m_3 \rightarrow 0\) then Equation (10)-(11) as derived from the Jacobian Coordinate Frame section simplifies to take on a similar form as the Two-Body Problem.

(1)\[\ddot{\mathbf{R}} = - G\frac{\left(m_1+m_2\right)}{R^3}\mathbf{R}\]

Many import results can be derived from this general form such as the analysis of the relative motion of the International Space Station, satellites, asteroids etc. among the Earth-Moon system.

Force Potential

Next, we can setup the total force potential as:

(2)\[U = \frac{Gm_1}{|\mathbf{r}+\frac{m_2}{m_1+m_2}\mathbf{R}|} + \frac{Gm_2}{|\mathbf{r}-\frac{m_1}{m_1+m_2}\mathbf{R}|} \]

so that

(3)\[\ddot{\mathbf{r}} = \frac{\partial{U}}{\partial{\mathbf{r}}}\]

In many scenarios, assume \(|\mathbf{R}|\) is constant such that \(P_1\) and \(P_2\) are in mutual circular orbit. This is certainly a valid assumption for systems such as Earth-Moon, or the Earth-Sun.

The Rotating Frame

In a rotating coordinate frame, the position vector for the Three-Body system can be represented as:

(4)\[\mathbf{R} = \left[ \cos\left(nt\right)\mathbf{\hat{x}}+ \sin\left(nt\right) \mathbf{\hat{y}} \right]\]

where \(n\) is the mean motion of the primary body system.

(5)\[n = \sqrt{\frac{G\left(m_1+m_2\right)}{R^3}} = n_{12}\]

Shift the coordinate system to a rotating frame so that \(\mathbf{R}\) is stationary along the local x-coordinate axis (\(\hat{\mathbf{x}}_R\)).

For example, consider the Earth-Moon system, the x-coordinate axis is always pointing from the Earth to the Moon and is rotating at a rate of \(\mathbf{n}\):

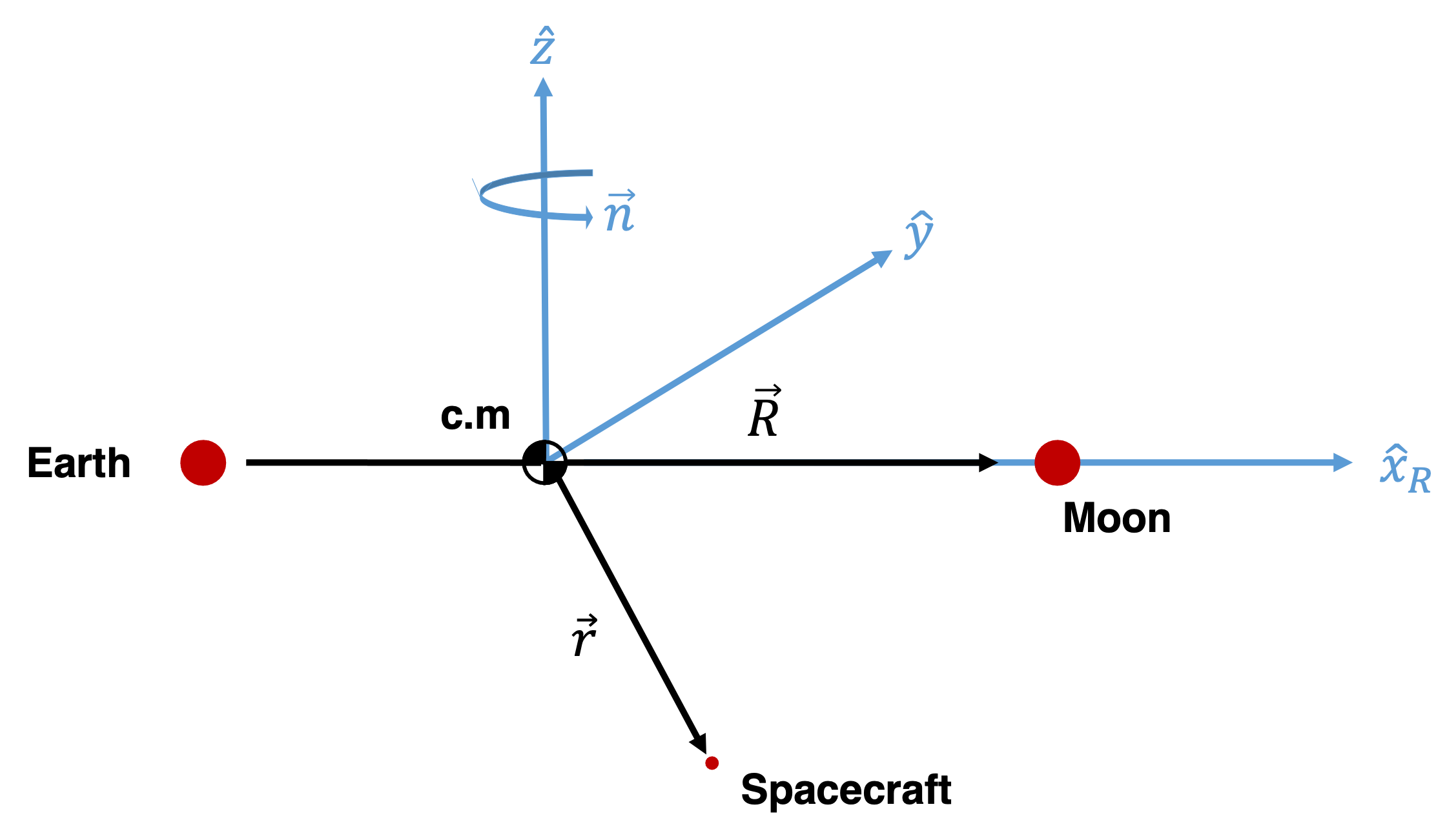
Figure 1.3 Jacobi Coordinate Frame Shifted to The Rotating Frame

The angular velocity (\(\Omega\)) for this system is defined as:

(6)\[\mathbf{\Omega} = n\mathbf{\hat{z}}\]

It is useful to relate the inerital position vector (\(\mathbf{r}_I\)) to the rotational vector (\(\mathbf{r}_R\)):

(7)\[\mathbf{r}_I = \mathbf{r}_R\]

The velocity in the inertial frame is:

(8)\[\dot{\mathbf{r}}_I = \dot{\mathbf{r}}_R + \mathbf{\Omega}\times\mathbf{r}_R\]

The acceleration in the inertial frame is:

(9)\[\ddot{\mathbf{r}}_I = \ddot{\mathbf{r}}_R + \dot{\mathbf{\Omega}}\times\mathbf{r}_R + 2\mathbf{\Omega}\times\dot{\mathbf{r}}_R+\mathbf{\Omega}\times\left(\mathbf{\Omega}\times\mathbf{r}_R \right)\]

Important

Note that \(\dot{\Omega} = 0\) since we assumed the orbit is circular. In other words \(n\) is constant.

Let \(\mathbf{r}_R\) be the position in the rotating coordinate frame. \(\mathbf{R}_R = \mathbf{r}\)

We can rewrite Equation (9) as:

\[\ddot{\mathbf{r}}_I = \ddot{\mathbf{r}} + 2\mathbf{\Omega}\times\dot{\mathbf{r}}+\mathbf{\Omega}\times\left(\mathbf{\Omega}\times\mathbf{r} \right) = \frac{\partial{U}}{\partial{\mathbf{r}}}\]

(10)\[\ddot{\mathbf{r}}_I = \ddot{\mathbf{r}} + 2n\mathbf{\hat{z}}\times\dot{\mathbf{r}} + n^2\mathbf{\hat{z}} \times \left( \mathbf{\hat{z}} \times \mathbf{r}\right)= \frac{\partial{U}}{\partial{\mathbf{r}}}\]

Equations of Motion

As part of the rotating coordinate frame, it is convenient to write Equation (10) in vector form by breaking [\(2n\mathbf{\hat{z}}\times\dot{\mathbf{r}}\)] and [\(n^2\mathbf{\hat{z}} \times \left( \mathbf{\hat{z}} \times \mathbf{r}\right)\)] into their components.

Thus, the set of equations of the Three-Body Problem for the circular restricted problem in the rotating coordinate frame are:

(11)\[ \begin{align}\begin{aligned}\ddot{x} - 2n\dot{y} = n^2x + \frac{\partial{U}}{\partial{x}}\\\ddot{y} + 2n\dot{x} = n^2y + \frac{\partial{U}}{\partial{y}}\\\ddot{z} = \frac{\partial{U}}{\partial{z}}\end{aligned}\end{align} \]

Note

The components of [\(2n\mathbf{\hat{z}}\times\dot{\mathbf{r}}\)] are usually referred to as the tidal terms in Astrodynamics. Think of this as \(P_2\) orbits \(P_1\) every orbital period there is a force experience directly as a function of \(n\)

\[\begin{split}\begin{matrix} - 2n\dot{y} \\ + 2n\dot{x} \\ \end{matrix} = \text{Tidal Terms}\end{split}\]

Simplifying The Equations of Motion

Equations (11) represent where the spacecraft is relative to the Jacobian Coordinate frame. Figure 1.4 below shows an updated frame of reference:

Figure 1.4 Circular Restricted Three-Body Problem in the Rotating Frame

Note

In Astrodynamics the mass ratios are generally defined as:

(12)\[\begin{split}\begin{align*} \mu &= \frac{m_2}{m_1+m_2} \\ 1 - \mu &= \frac{m_1}{m_1+m_2} \end{align*}\end{split}\]

The total force potential (2) for this system can be rewritten as:

(13)\[U\left(\mathbf{r} \right) = \frac{Gm_1}{\sqrt{\left( x + \frac{m_2}{m_1+m_2}R \right)^2+y^2+z^2}} + \frac{Gm_2}{\sqrt{\left( x - \frac{m_1}{m_1+m_2}R \right)^2+y^2+z^2}}\]

Let us write this a bit more concisely by defining a new force potential as \(\mathbf{V}\) in order to simplify our equations of motion Equation (11):

(14)\[\mathbf{V}\left(x,y,z\right) = \frac{1}{2}n^2\left( x^2 + y^2 \right) + \mathbf{U}\]

(15)\[\mathbf{U} = \frac{Gm_1}{r_1} + \frac{Gm_2}{r_2}\]

where \(r_1\) and \(r_2\) are:

\[r_1 = \sqrt{\left( x + \frac{m_2}{m_1+m_2}R \right)^2+y^2+z^2}\]

\[r_ 2 = \sqrt{\left( x - \frac{m_1}{m_1+m_2}R \right)^2+y^2+z^2}\]

Note

The potential energy is made up of three components

1. The potential energy due to the force induced by the rotating reference frame

2. The gravitational potential energy from \(P_1\)

3. The gravitational potential energy from \(P_2\)

Figure 1.5 below is an example of solving Force Potential (14) for the Earth-Moon system. The figure is interactive and generated using Plotly, an open-source graphing library for Python. The reader is encouraged to interact with Figure 1.5 using their mouse to zoom into the region of space around the bodies and rotate the surface to inspect the potential wells.

Figure 1.5. Example of CR3BP Potential

Equations of Motion

Finally, the generalized equations of motion for the Circular Restricted Three-Body Problem are:

(16)\[\begin{split}\begin{align*} \ddot{x} - 2n\dot{y} &= \frac{\partial{\mathbf{V}}}{\partial{x}} \\ \ddot{y} + 2n\dot{x} &= \frac{\partial{\mathbf{V}}}{\partial{y}} \\ \ddot{z} &= \frac{\partial{\mathbf{V}}}{\partial{z}} \end{align*}\end{split}\]